PRODUIT VECTORIEL


Définitions
Interprétation géométrique
Applications

















































Définitions


       Produit vectoriel
       Propriétés

Produit vectoriel

       Le produit vectoriel de deux vecteurs v1 et v2, dans un repère orthonormé, est le vecteur, défini par: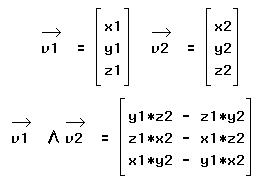


Propriétés

        Le produit vectoriel n´est pas commutatif, mais alterné:


        Distributivité par rapport à l´addition:


        Produit par un scalaire:


        Pour que le produit vectoriel de deux vecteurs soit nul il faut et il suffit que ces vecteurs soient liés (par une combinaison linéaire):


       En particulier si l´un des vecteurs est nul le produit vectoriel est nul.

Interprétation géométrique

        Le produit vectoriel de deux vecteurs v1 et v2 (non nuls et non collinéaires) est le vecteur v3 perpendiculaire à leur plan tel que le trièdre (v1,v2,v3) soit direct, et dont le module est égal au produit des modules de v1 et v2 par le sinus de leur angle, qui est aussi l´aire du parallélogramme construit sur v1 et v2.



        En particulier le produit vectoriel de deux vecteurs unitaires a pour module le sinus de leur angle.
        Remarque: On appelle trièdre direct un triplet (v1,v2,v3) de vecteurs de l´espace linéairement indépendants dont l´orientation est donné par la règle du tire-bouchon (Lorsque l´on visse un tire-bouchon le long de v3, il tourne de v1 vers v2)


Applications


       Trièdre
       Normale à une surface paramétrique
       Calcul d´un angle
       Normale à une facette

Trièdre direct

        Si v1 et v2 sont deux vecteurs non collinéaires, alors leur produit vectoriel v3 détermine un trièdre direct (v1,v2,v3). Pour en faire un trièdre orthonormé:
        Déterminer un vecteur w2 perpendiculaire à v1 dans le plan (v1,v2)
        Calculer v3 = vectoriel(v1,w2)
        Normaliser: v1 = v1 / ||v1||, w2 = w2 / ||w2|| et v3 = v3 / ||v3||
        Le trièdre (v1,w2,v3) est alors direct et orthonormé.

Normale à une surface paramétrique

        Soit une surface paramétrique définie par:
                x = f(u,v)
                y = g(u,v)
                z = h(u,v)
        On montre que le vecteur tangent en M0(u0) à une courbe paramétrique M=M(u) est la dérivée de M par rapport à u: T = dM / du. On appelle dérivée partielle d´une fonction de plusieurs variables M(u,v) par rapport à l´une des variables, la dérivée de cette fonction lorsque les autres variables sont constantes.
        Le vecteur tangent en M0(u0,v0) à la courbe en u (v = v0 constant) est donc la dérivée partielle de M par rapport à u, de même le vecteur tangent à la courbe en v (u = u0 constant) est la dérivée partielle de M par rapport à v.





        Un vecteur normal à la surface est le produit vectoriel de ces deux vecteurs tangents.


Calcul d´un angle

        Pour calculer l´angle an de deux vecteurs v1 et v2:
        Leur produit vectoriel permet de calculer s=sin(an) à PI près (voir l´interprétation géométrique du produit vectoriel), d´où:
                an1 = asin(s) ou an2 = PI - asin(s)
        Leur produit scalaire permet de lever l´indétermination:
                si c>0 an = an1, sinon an = an2

Normale à une facette

        Dans un volume polyédrique, les facettes sont décrites de telle façon que les normales soient orientées vers l´extérieur.
        Si la facette est triangulaire (P1,P2,P3), une normale à son plan est:



        Mais si la facette n´est pas triangulaire, outre qu´elle n´est pas nécéssairement plane, sa normale peut être inversée comme le montre la figure suivante:


        Pour éviter cette inversion, on calcule la normale comme la moyenne des produits vectoriels des couples d´arêtes de la facette. Une formule efficace est:


Avec: si i#n alors j=i+1, sinon j=1
        Exemple:





        Qui est bien un vecteur direct quand on tourne sur la facette dans le sens (P1,P2,P3,P4), alors que le produit vectoriel de P1P2 par P2P3 donne un vecteur dans l´autre sens.